画像をダウンロード 1次関数 傾き 求め方 594098-1次関数 傾き 切片 求め方
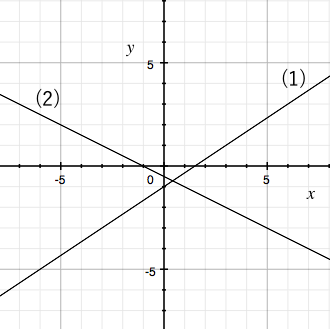
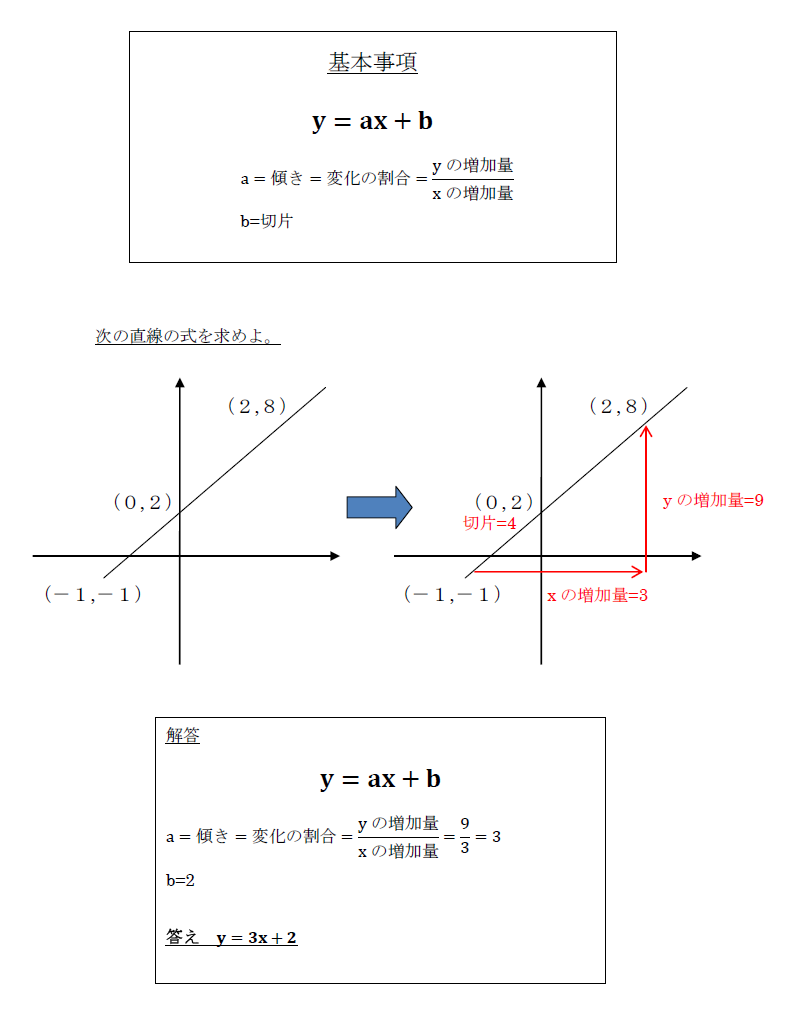
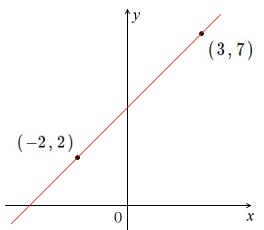
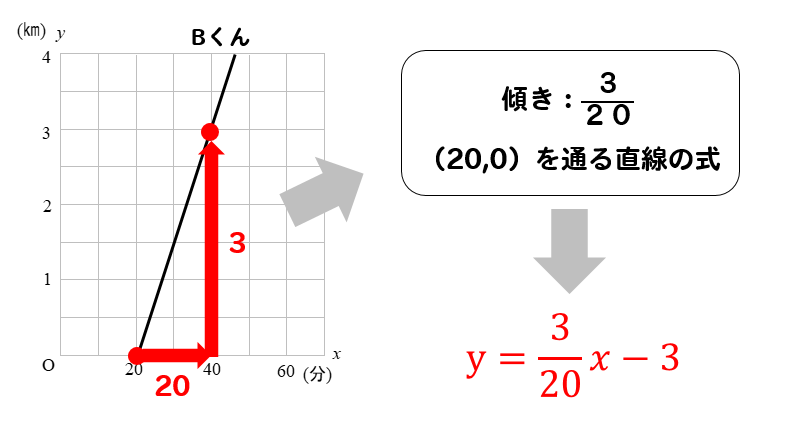
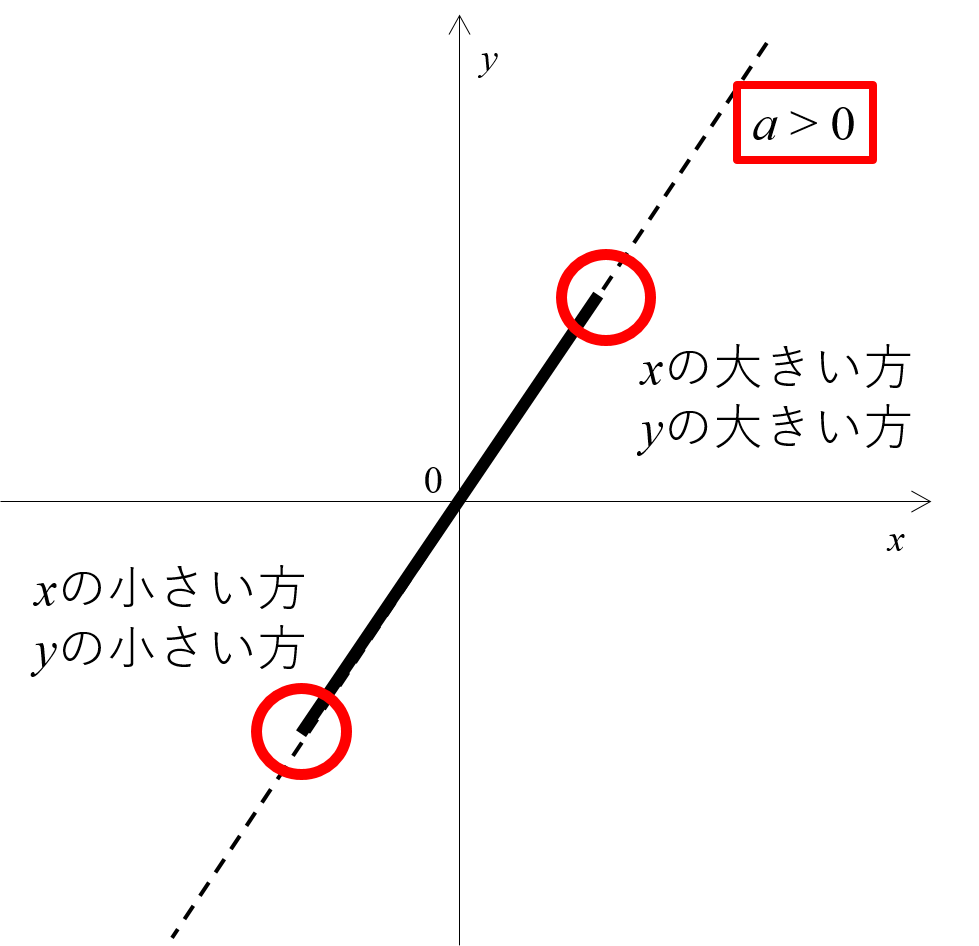
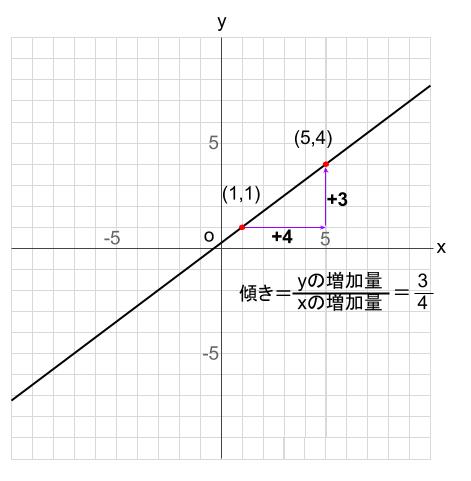
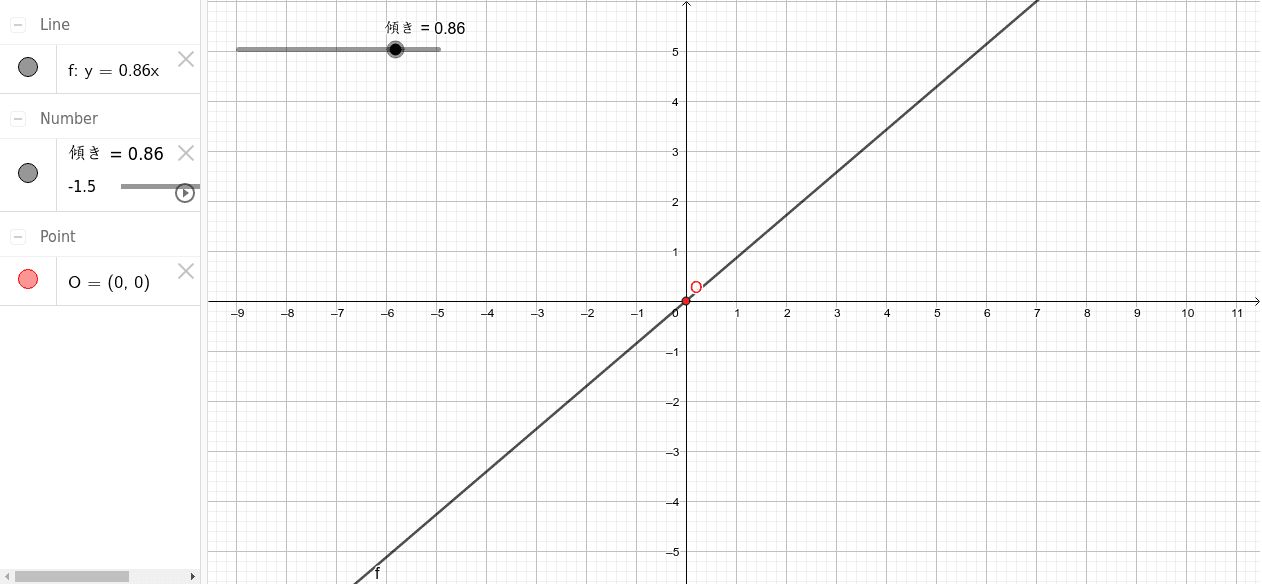
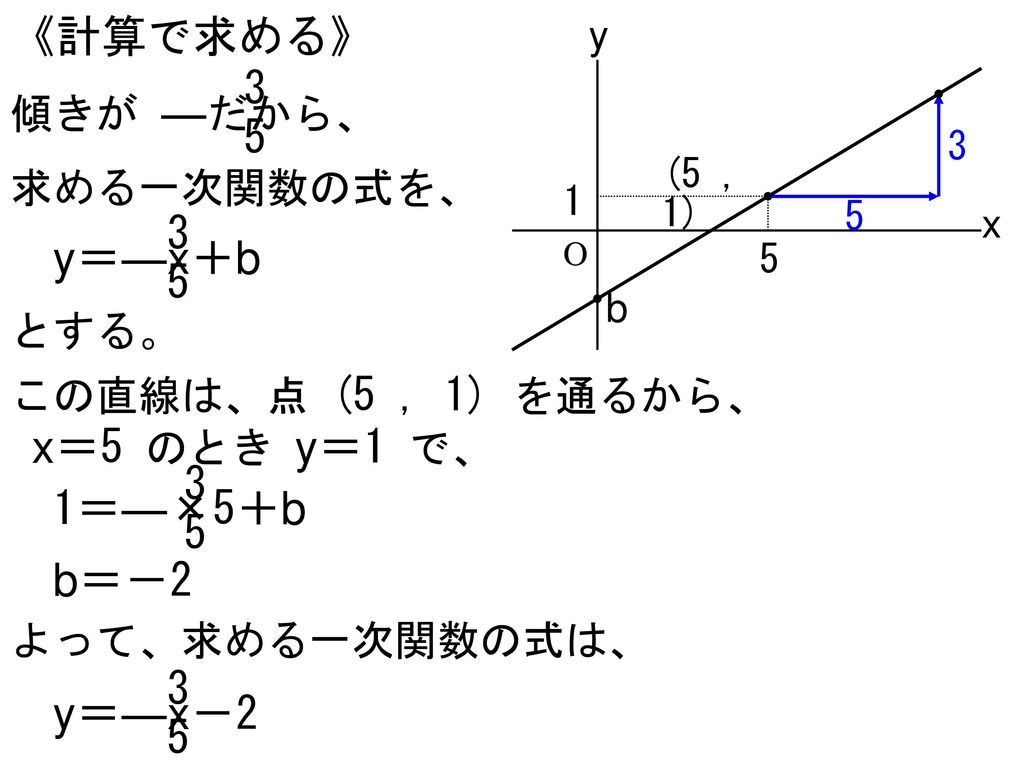
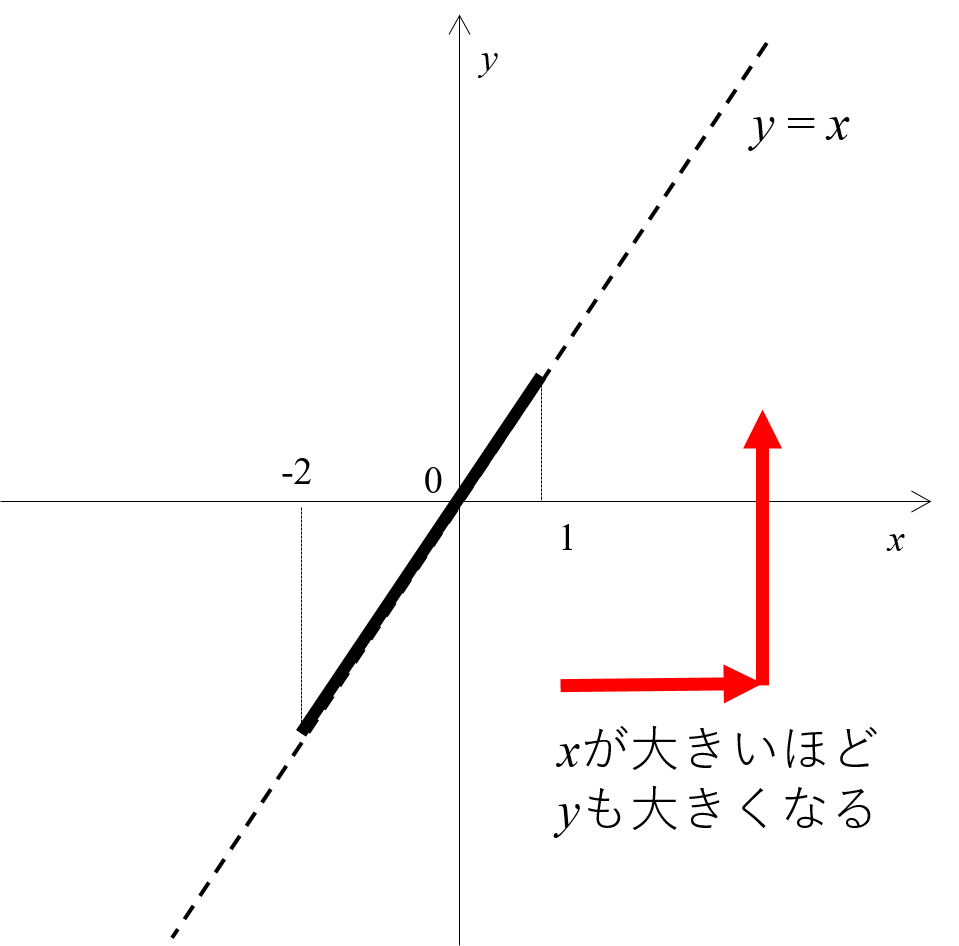
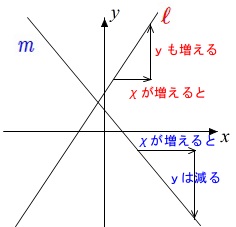
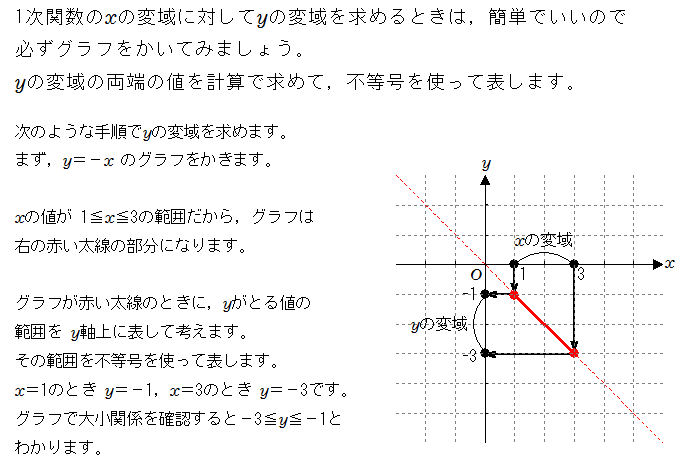
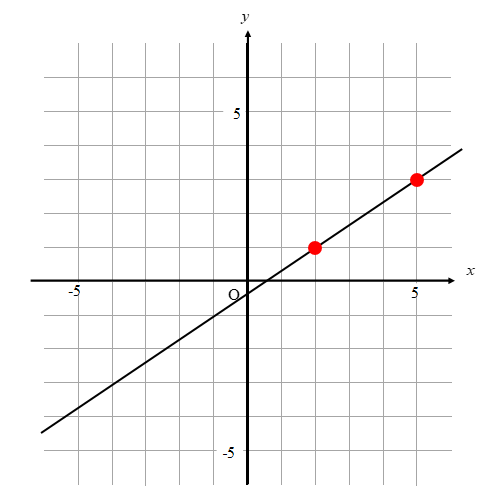
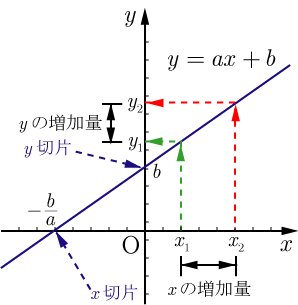
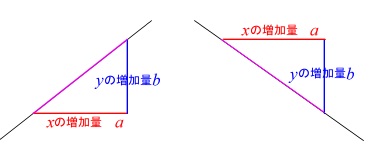
1次関数では変化の割合と傾きが同じ 変化の割合は \(\displaystyle \,\color{red}{変化の割合=\frac{ (\,y\,の増加量) }{ (\,x\,増加量) }}\,\) となりますが、 \(\,1\,\)次関数は直線なので傾きがこの変化の割合に一致します。 \(\,1\,\)次関数で
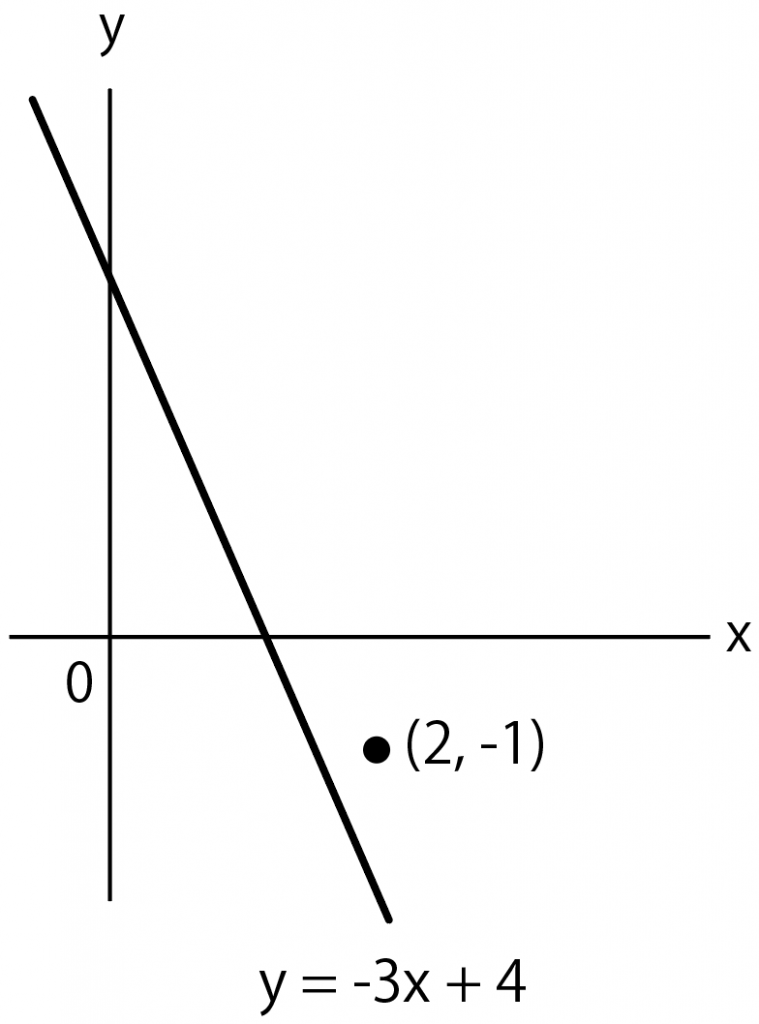
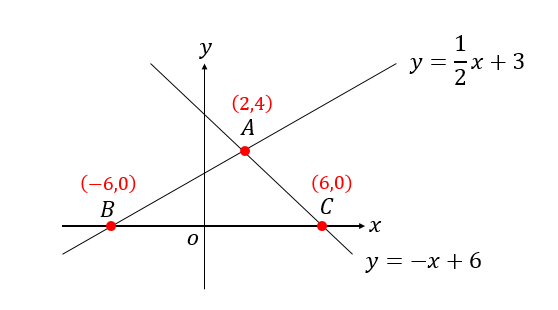
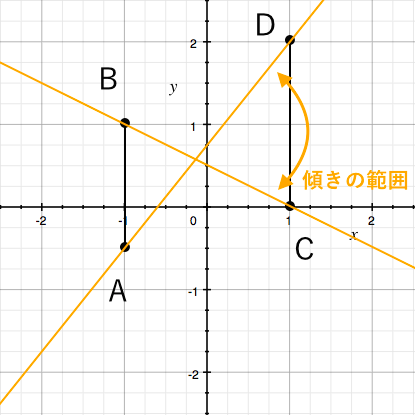
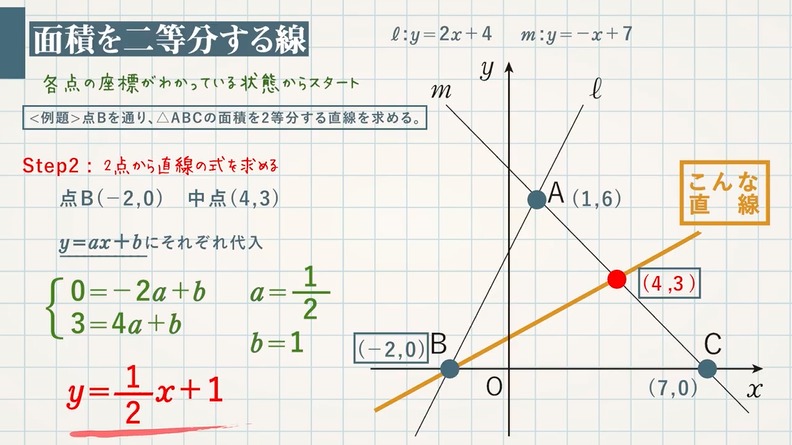
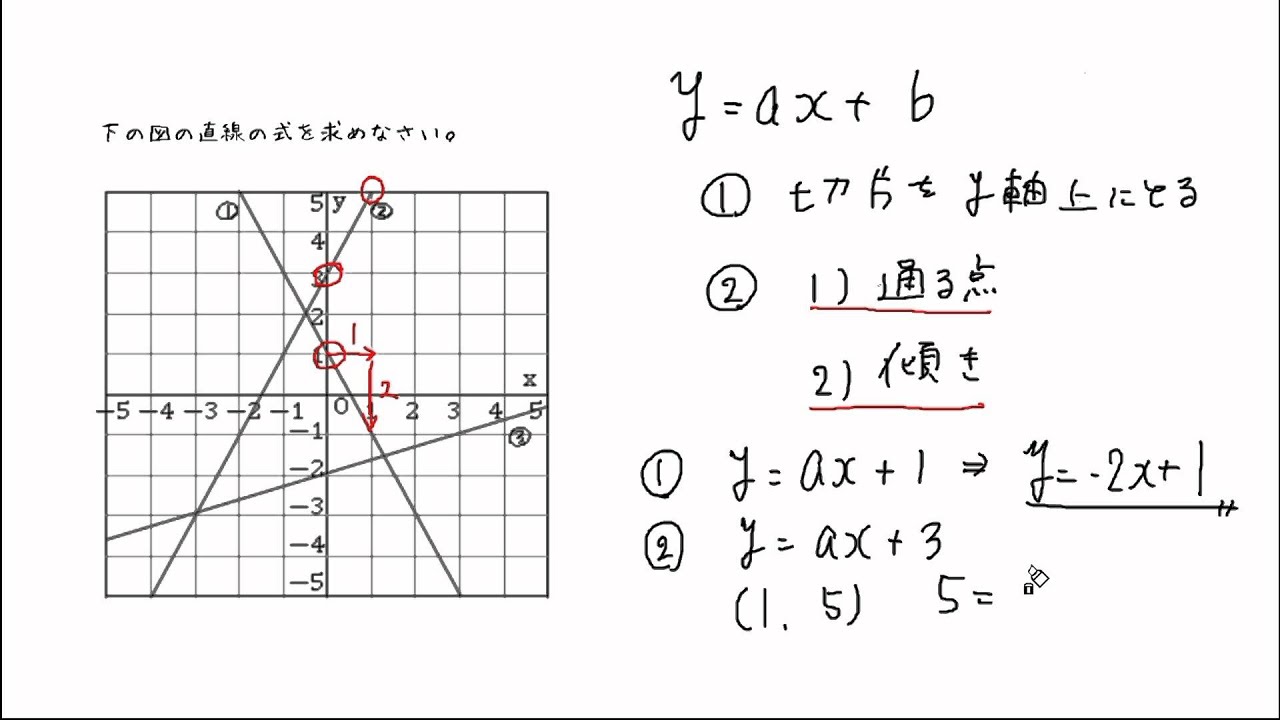
1次関数 傾き 切片 求め方- 一次関数 (三角形の面積) 中2数学 一次関数の発展問題です。 式の求め方や座標の求め方がしっかり定着していないと難しいので、まずはその練習をしっかりしておいてくだ 条件を満たす直線の中で傾きが一番小さいものは点bを通る時で、傾きが一番大きいものは点aを通る時だとわかります。 そして、直線の傾きがその最大と最小の間にある時だけ 直線\(y=ax+4\)が線分AB(両端)と交わっています 。
1次関数 傾き 切片 求め方のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 | ||
 |  | |
 |  |  |
「1次関数 傾き 切片 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「1次関数 傾き 切片 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
 |  |  |
「1次関数 傾き 切片 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
 |  |  |
「1次関数 傾き 切片 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
 | ||
「1次関数 傾き 切片 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
 |  |  |
「1次関数 傾き 切片 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 | 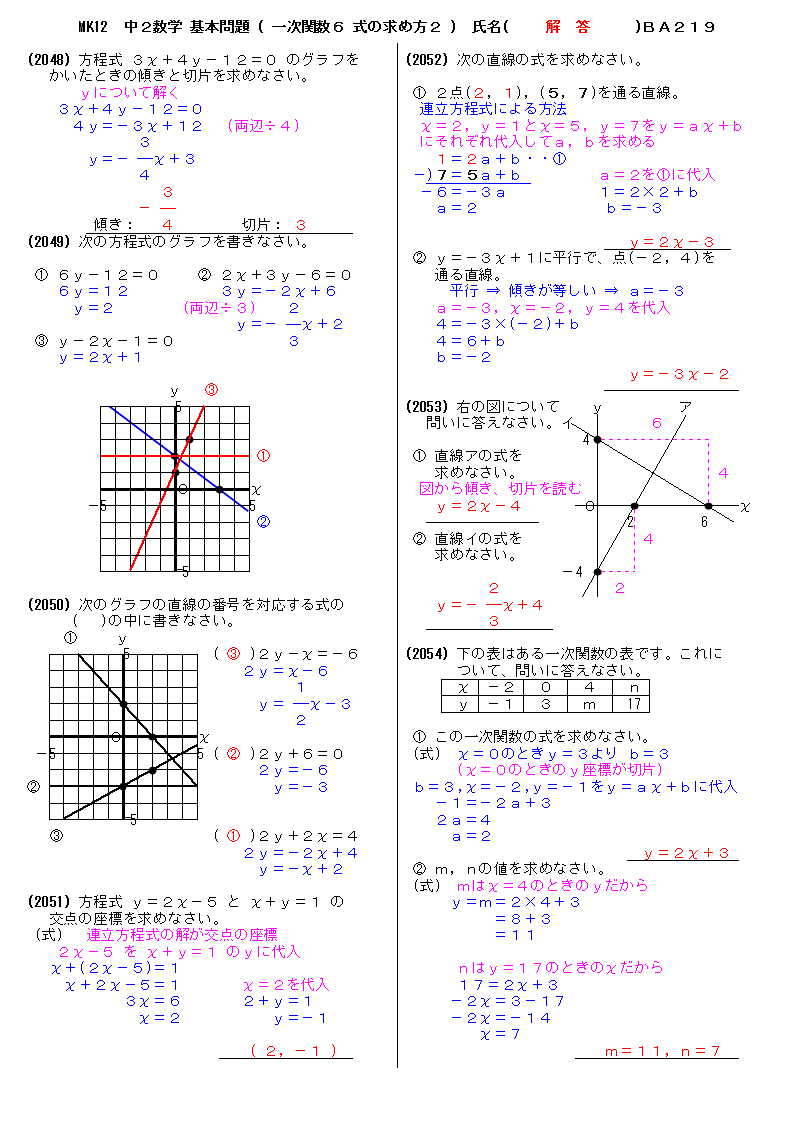 |  |
 |  | |
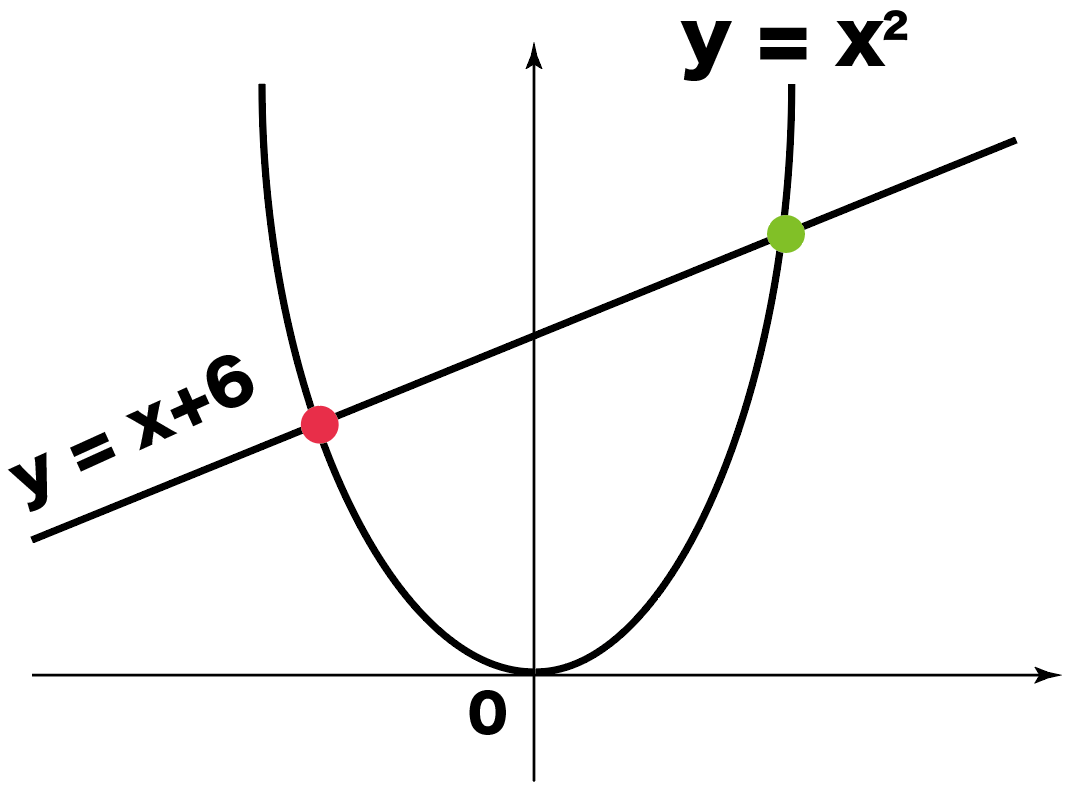 |  | |
 |  |  |
「1次関数 傾き 切片 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  | |
「1次関数 傾き 切片 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
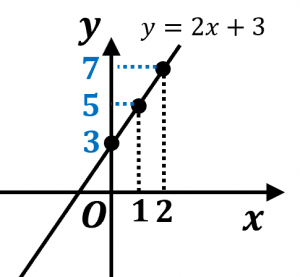 |  |
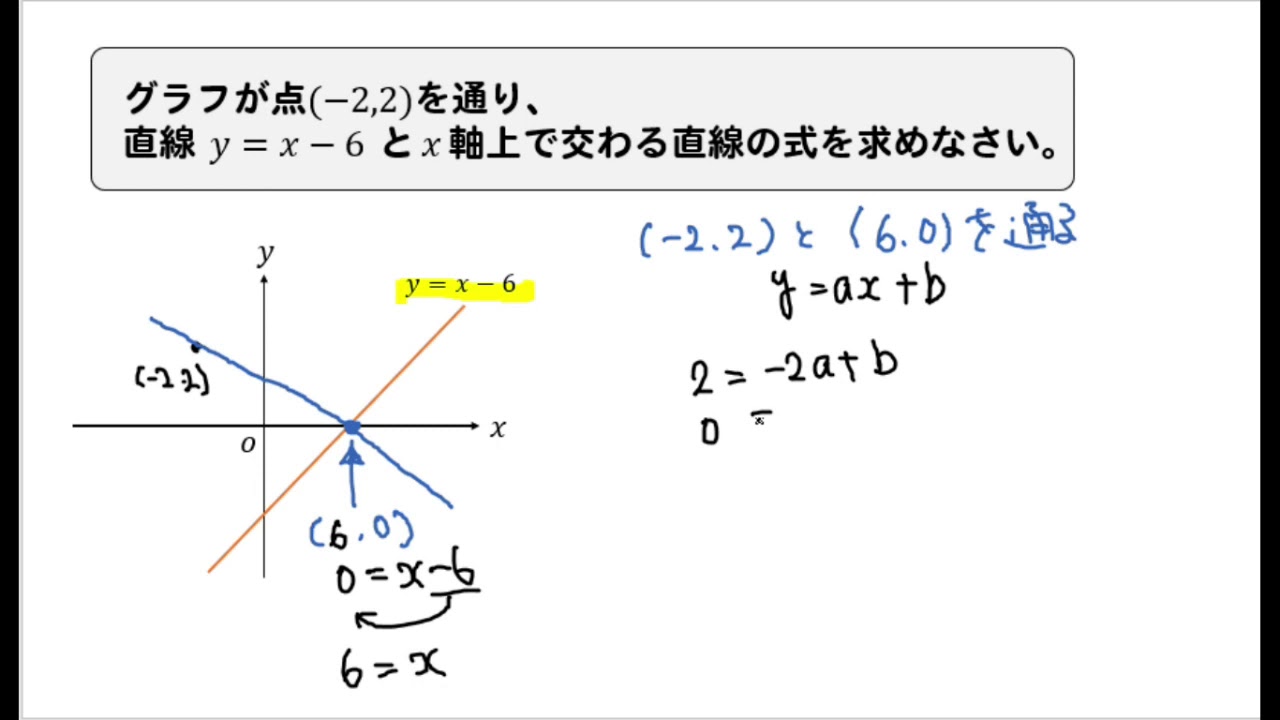
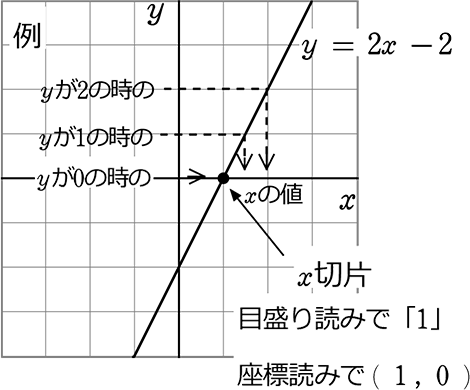
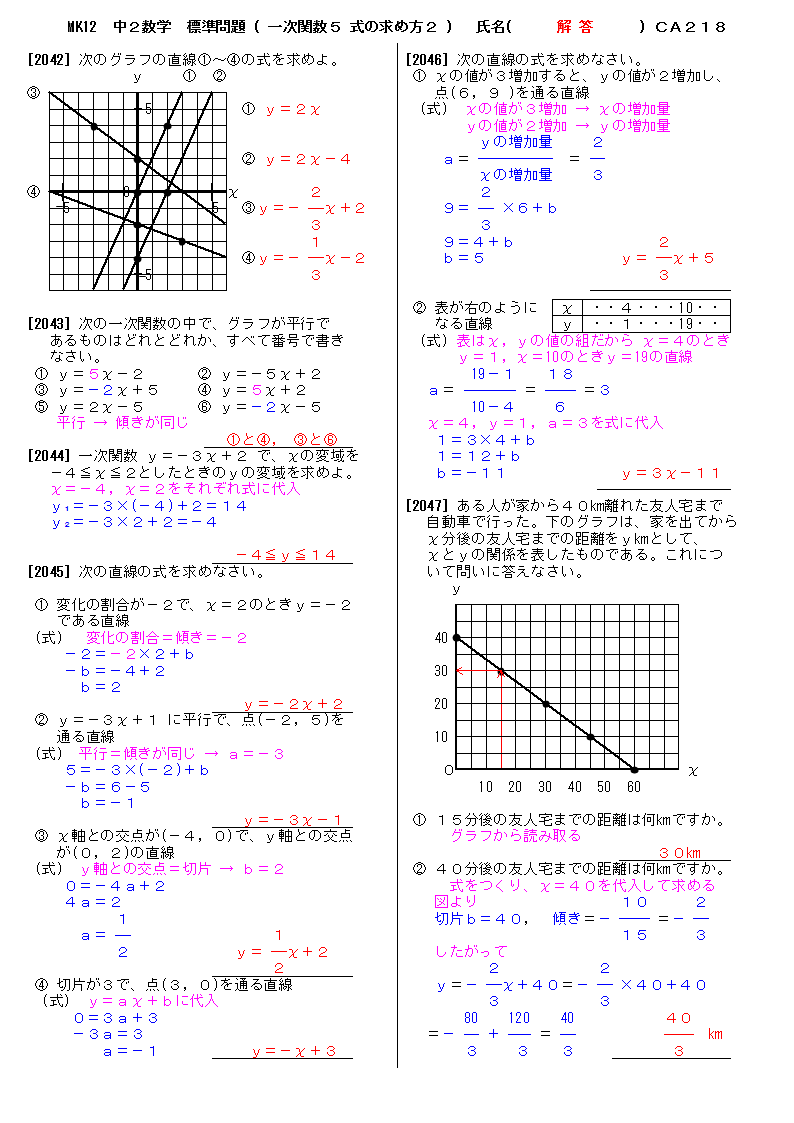
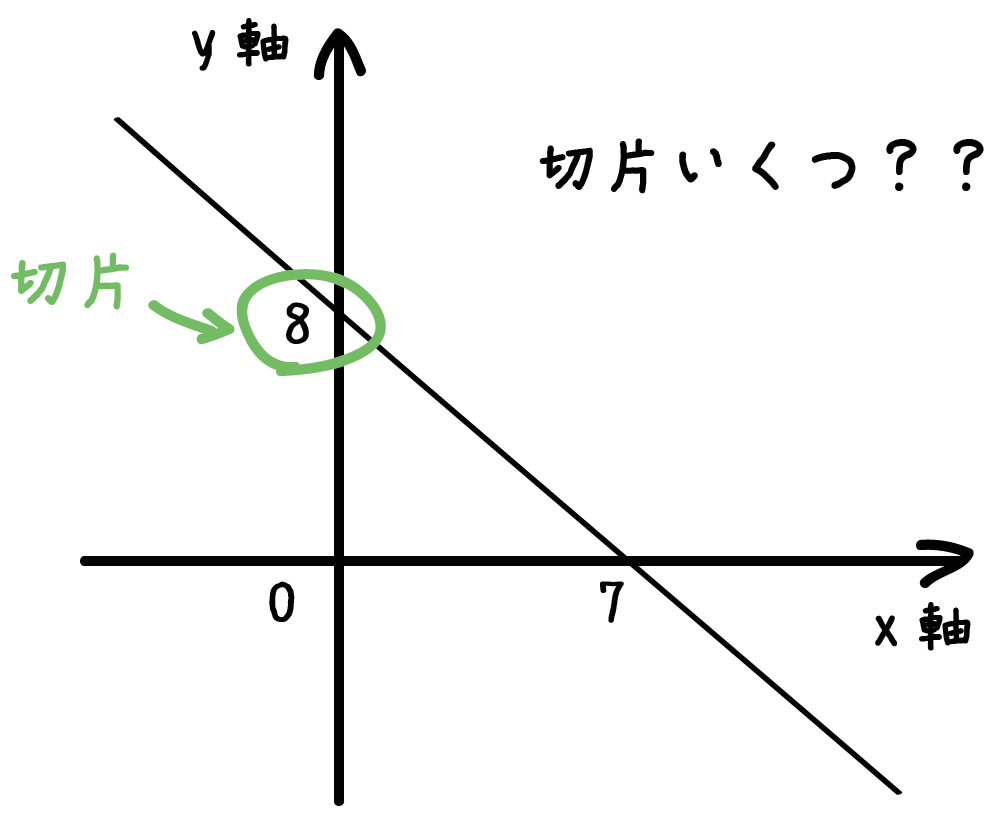
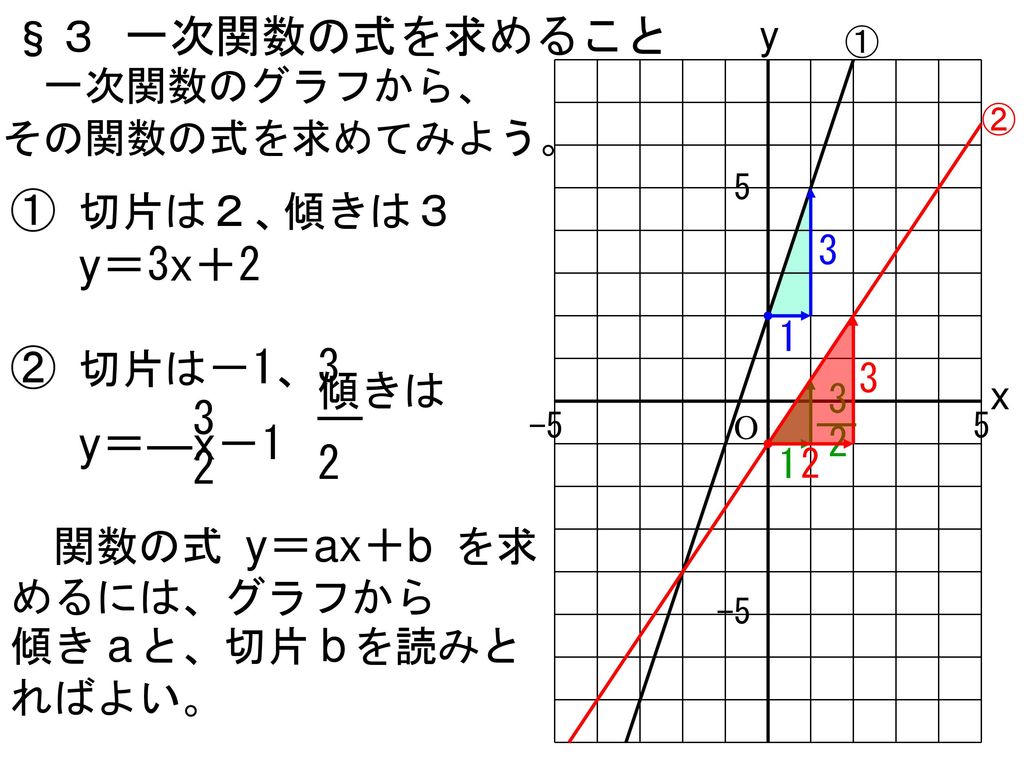
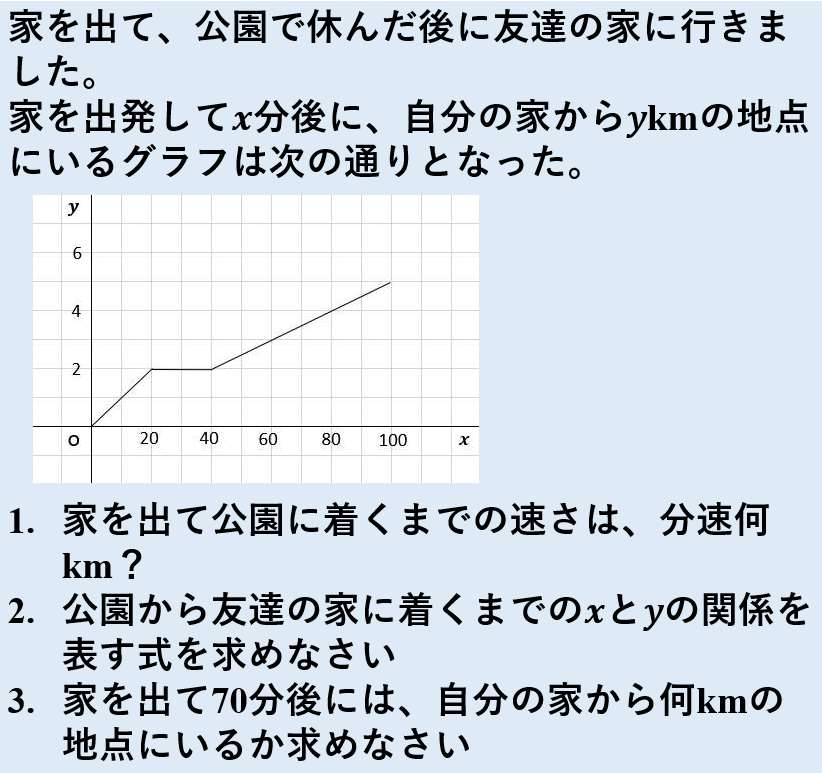
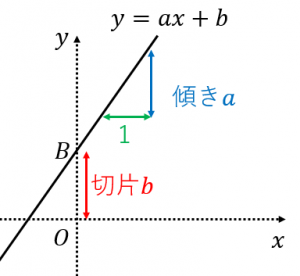
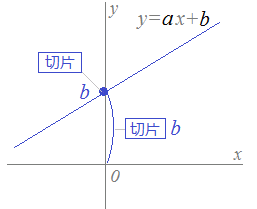
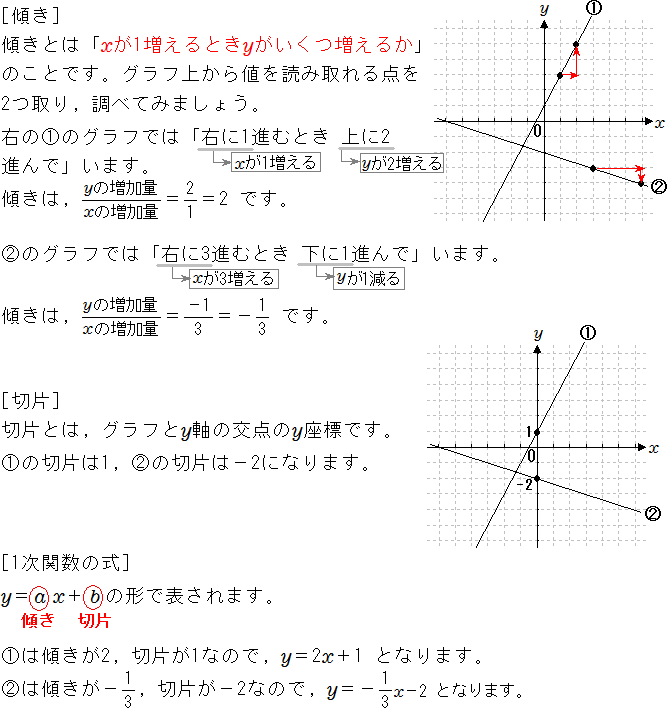
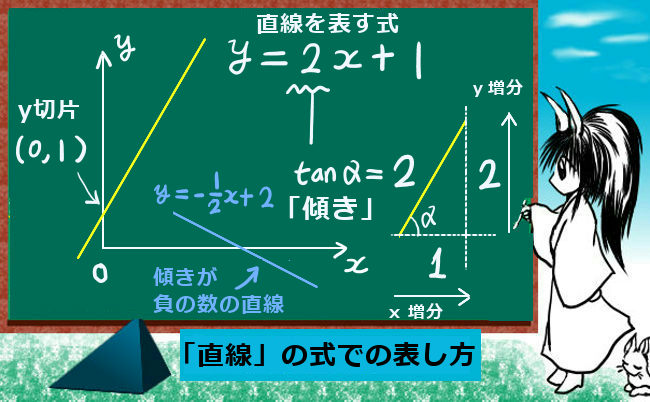
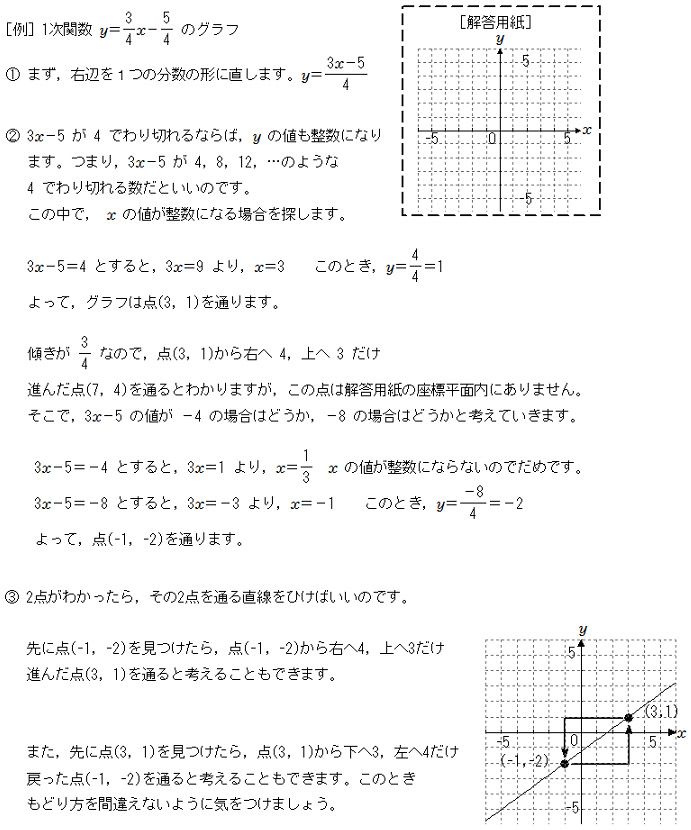
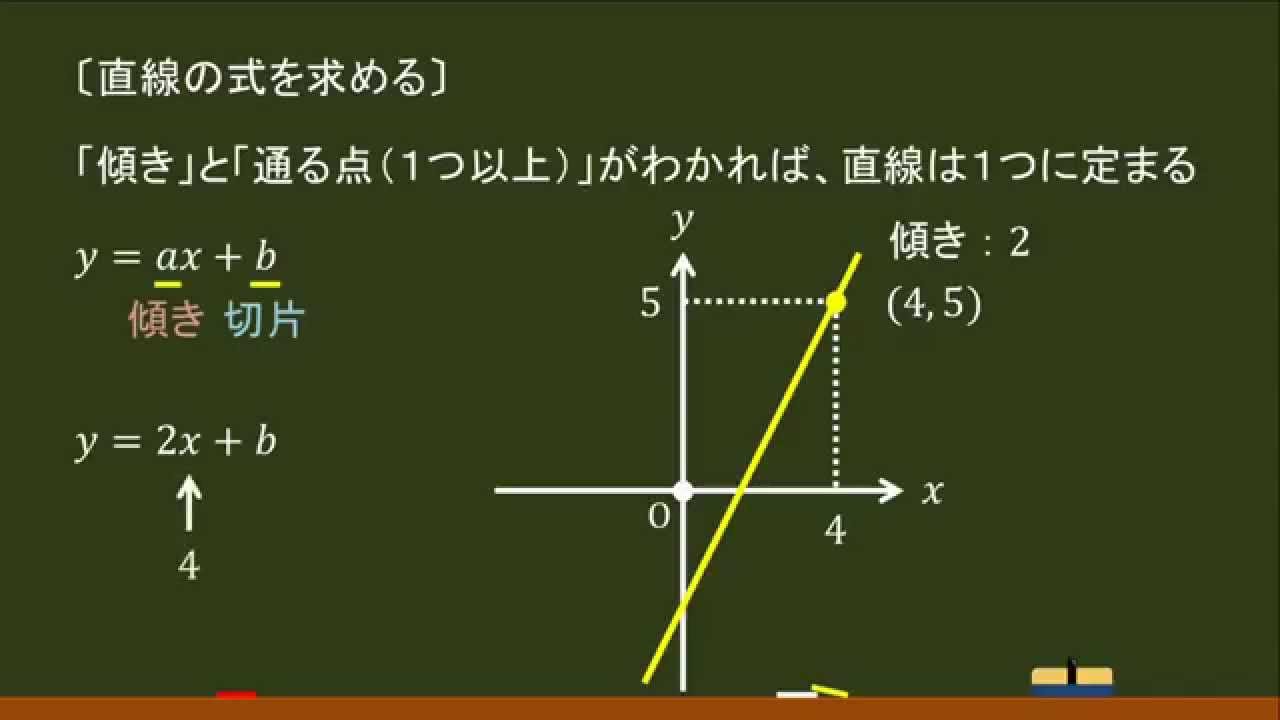
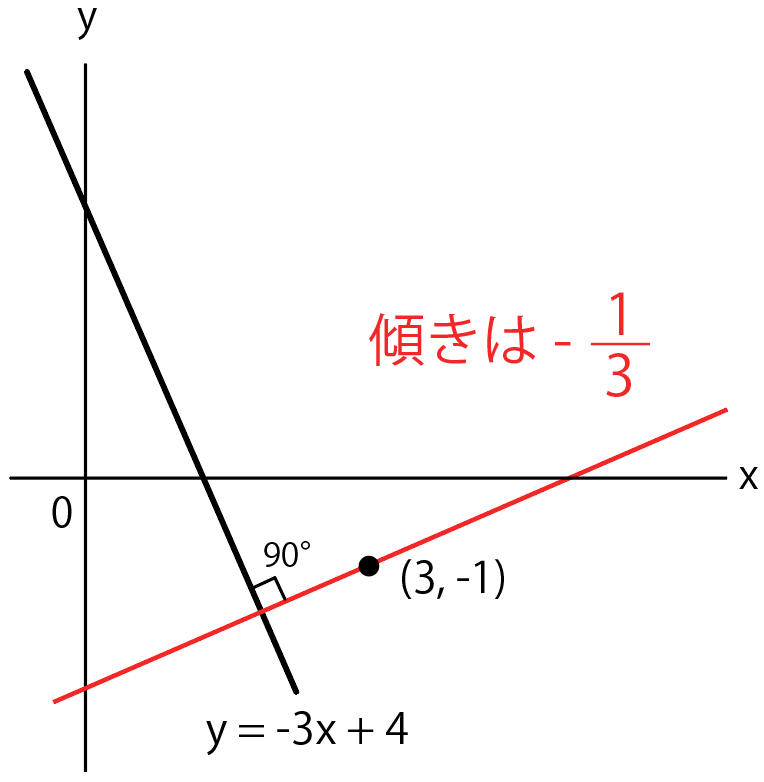
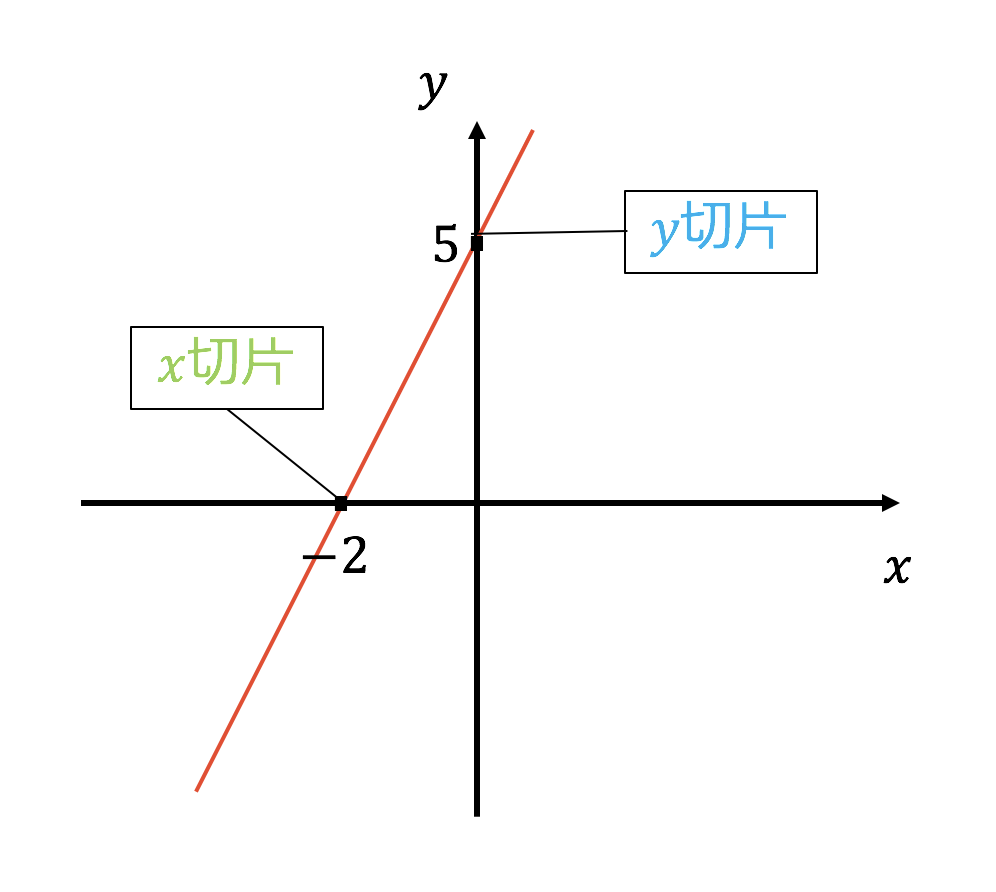
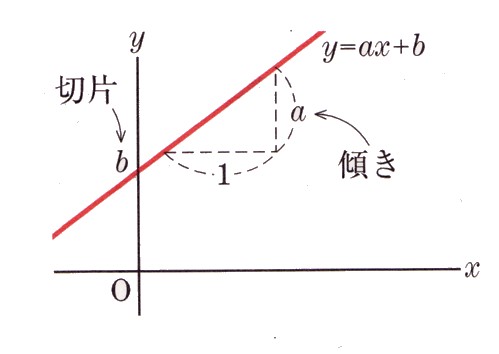
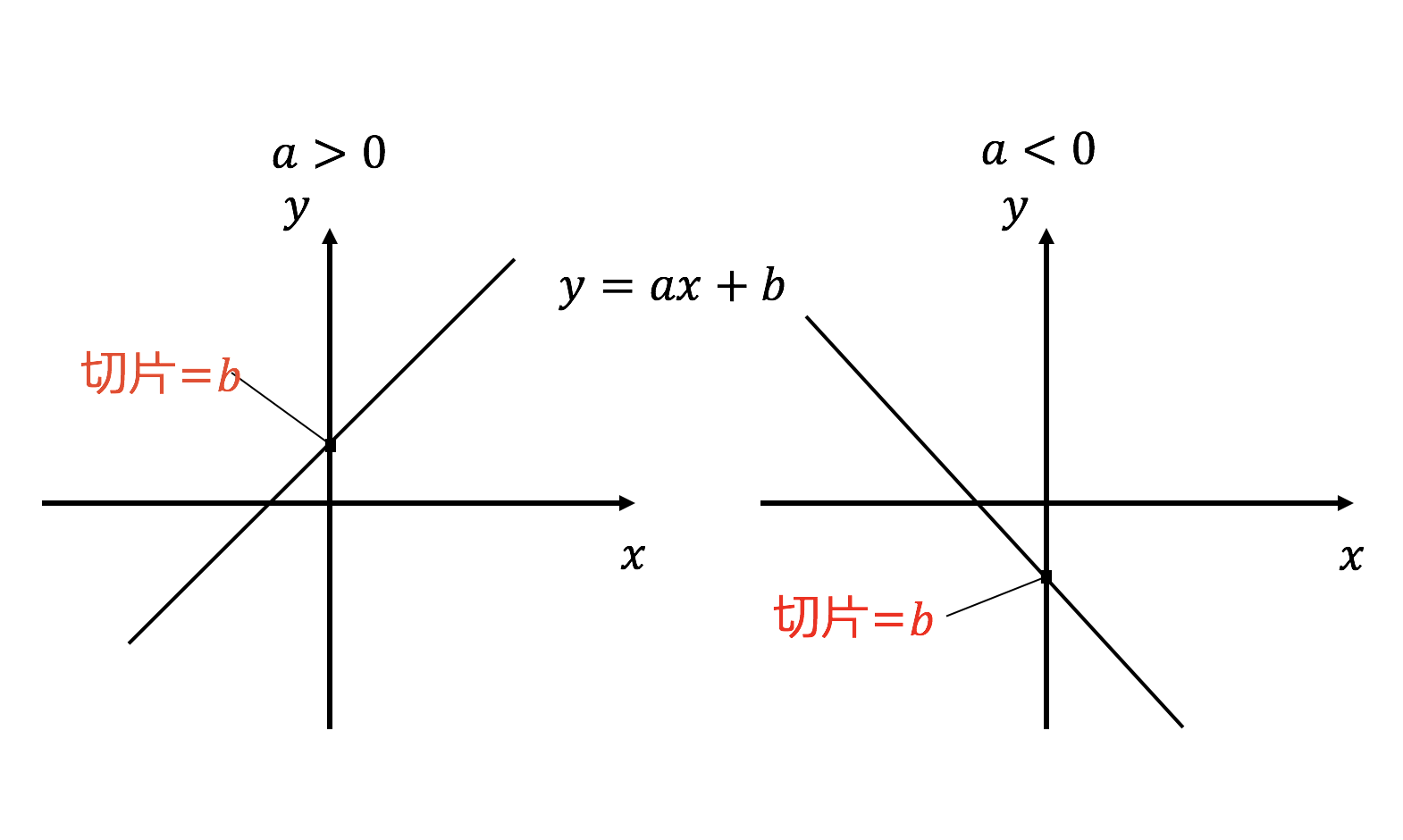
一次関数 y = ax b の a を傾き、b を切片という。a はグラフの傾き、b はグラフと y 軸の交点を意味します。 例題 次の関数の傾きと切片を求めなさい。 (1) y = 2x 3 (2) y = 5x 1 (3) y = 3x 9 (4) y = 5/2x 4 (5) y = 3 解答 (1) 傾き 2 切片 3 (2) 傾き 5 切片 1 (3) 傾き 3最小二乗法とは 最小二乗法(または、最小自乗法)とは、誤差を伴う測定値の処理において、その誤差の二乗の和を最小にすることで、最も確からしい関係式を求める方法です。 ここでは、最小二乗法によって回帰直線(1 次関数
Incoming Term: 1次関数 傾き 求め方, 1次関数 傾き 切片 求め方,
コメント
コメントを投稿